개요
classDiagram ISpatial--|>IMeshSpatial IMeshSpatial--|>TMeshAABBTree3
TMeshAABBTree3는 메쉬를 구성하는 삼각형들을 공간으로 분할하여 트리로 담아두기 위한 자료구조이다.
자료구조 설명
트리 구조
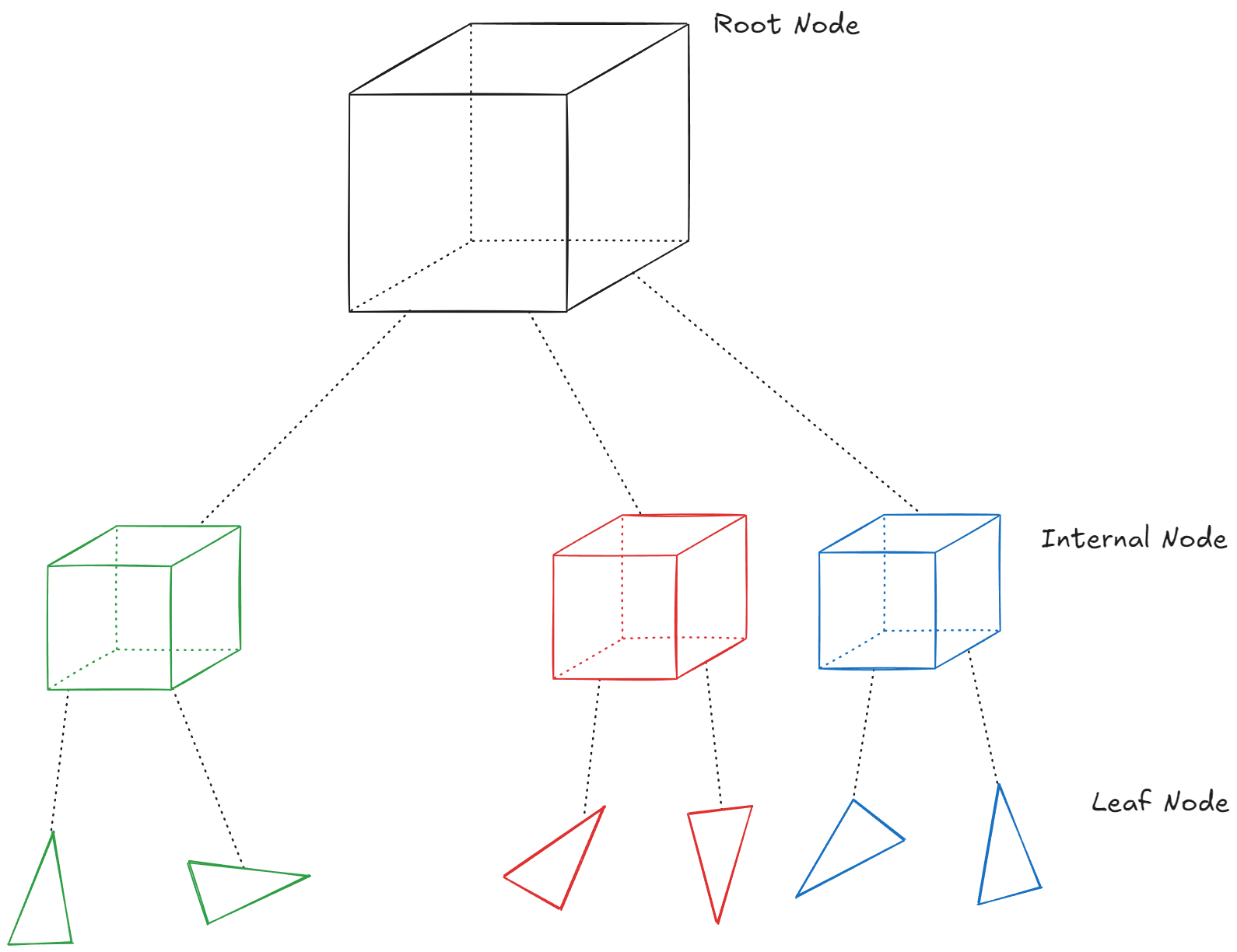
| 노드 타입 | 설명 |
|---|---|
| Root ( 루트 ) | 전체 메시를 감싸는 최상위 박스 |
| Internal Nodes ( 내부 노드 ) | 1~2개의 자식 박스를 가짐 |
| Leaf Nodes ( 리프 노드 ) | 실제 삼각형들을 저장 ( 기본 3개 이하 ) |
핵심 데이터 구조
TDynamicVector< int > BoxToIndex; // 박스 → IndexList 포인터
TDynamicVector< FVector3d > BoxCenters; // 박스 중심점
TDynamicVector< FVector3d > BoxExtents; // 박스 크기 (절반)
TDynamicVector< int > IndexList; // 삼각형 ID 또는 자식 박스 ID
int TrianglesEnd; // 삼각형/노드 경계 인덱스
int RootIndex; // 루트 박스 인덱스IndexList의 자료 구조
IndexList는 삼각형의 ID 혹은 TAxisAlignedBox3의 ID를 담는다. 그리고 담는 ID에 따라 구조가 약간씩 다르다.
리프 노드 ( 삼각형 목록 )
idx < TrianglesEnd 인 경우:
[N, t1, t2, t3, ..., tN]
↑ ↑ ↑ ↑
| | | |
| +---+---+-- 삼각형 ID들
+-- 삼각형 개수
내부 노드 - 자식 1개
idx >= TrianglesEnd && IndexList[idx] < 0 인 경우:
[-child_idx - 1]
↑
음수로 인코딩된 자식 박스 인덱스
내부 노드 - 자식 2개
idx >= TrianglesEnd && IndexList[idx] > 0 인 경우:
[child1_idx + 1, child2_idx + 1]
↑ ↑
첫 번째 자식 두 번째 자식 (모두 +1 오프셋)
내부 노드를 담는 경우 -1 / +1오프셋을 이용하는 이유는 실제 인덱스 0과 구분을 하기 위함이다.
주요 기능
가장 가까운 삼각형 찾기
int FindNearestTriangle
(
const FVector3d& P, // 검색할 점
double& NearestDistSqr, // [출력] 거리²
const FQueryOptions& Options // 옵션
) const- 루트부터 시작
- 리프 노드면: 모든 삼각형과의 거리 계산
- 내부 노드면:
- 가까운 자식부터 탐색 ( 가지치기 최적화 )
- 현재 최소 거리보다 먼 박스는 스킵
탐색 예시
Root
/ \
[5.0] [3.2] ← 박스까지 거리
↓
[3.2] 를 먼저 탐색 (더 가까움)
/ \
[2.1] [4.5]
↓
[2.1] 탐색 → 삼각형 발견 (거리 2.5)
이제 최소거리 = 2.5
[4.5]는 스킵 (4.5 > 2.5)
[5.0]도 스킵 (5.0 > 2.5)
레이 교차 검사
bool FindNearestRayTriangleIntersection
(
const FRay3d& Ray, // 레이
double& NearestT, // [출력] 교차 거리
int& TID, // [출력] 삼각형 ID
FVector3d& BaryCoords // [출력] 무게중심 좌표
) const- 마우스 클릭으로 메시 표면 선택
- 총알/광선의 충돌 감지
- 시야 차단 확인 ( visibility )
메시-메시 교차 검사
bool TestIntersection
(
const TMeshAABBTree3& OtherTree, // 다른 메시 트리
const TFunction< FVector3d( const FVector3d& ) >& TransformF // 변환 함수
) const- 두 트리를 동시에 탐색
- 박스가 겹치지 않으면 스킵
- 리프까지 도달하면 삼각형-삼각형 교차 검사
트리 순회
struct FTreeTraversal
{
// 박스 방문 시 호출
TFunction< bool( const FAxisAlignedBox3d&, int ) > NextBoxF;
// 리프 노드의 삼각형들 처리
TFunction< void( int ) > TriangleF;
};
void DoTraversal( FTreeTraversal& Traversal ) const- 특정 영역 내 모든 삼각형 수집
- 메시 통계 계산
- 커스텀 공간 쿼리
트리 구축
Build 과정
void Build()
{
BuildTopDown( false );
MeshChangeStamp = Mesh->GetChangeStamp();
}Top-Down 구축 알고리즘
- 모든 삼각형의 중심점 계산
- 재귀적 분할:
- 삼각형 수 ≤ TopDownLeafMaxTriCount ( 기본 3 )면 리프 생성
- 아니면:
- 가장 긴 축 ( X/Y/Z ) 선택
- 중간점 기준으로 삼각형들을 왼쪽/오른쪽 분할
- 각 절반에 대해 재귀 호출
- 박스 정보 저장 ( 중심, 크기 )
축 선택 전략
GetSplitAxis = [] ( int Depth, const FAxisAlignedBox3d& )
{
return Depth % 3; // 0=X, 1=Y, 2=Z 순환
};성능 최적화 기법
가지치기 ( Pruning )
// 박스까지 거리가 현재 최소거리보다 크면 스킵
if ( BoxDistanceSqr( ChildBox, P ) > NearestDistSqr )
return; // 탐색 안 함가까운 자식 우선 탐색
if ( fChild1DistSqr < fChild2DistSqr )
{
// Child1 먼저 탐색
find_nearest_tri( iChild1, P, NearestDistSqr, TID );
// 그 다음 Child2 (필요하면)
if ( fChild2DistSqr < NearestDistSqr )
find_nearest_tri( iChild2, P, NearestDistSqr, TID );
}Early Exit
bool IsWithinDistanceSquared
(
const FVector3d& Point,
double ThresholdDistanceSqr, // 이 거리 이내에 있으면 즉시 종료
int& OutTriangleID
) const박스 확장 ( Epsilon )
FAxisAlignedBox3d GetBoxEps( int IBox, double Epsilon ) const
{
FVector3d e = BoxExtents[ IBox ];
e[ 0 ] += Epsilon; // 수치 오차 보정
e[ 1 ] += Epsilon;
e[ 2 ] += Epsilon;
return FAxisAlignedBox3d( c - e, c + e );
}실제 사용 예시
메시 표면에 점 투영
TMeshAABBTree3< FDynamicMesh3 > Tree( &MyMesh );
Tree.Build();
FVector3d SurfacePoint = Tree.FindNearestPoint( MyPoint );
// SurfacePoint = 메시 표면의 가장 가까운 점레이캐스팅 ( 마우스 피킹 )
FRay3d MouseRay = GetMouseRay();
double HitDistance;
int HitTriangleID;
FVector3d BaryCoords;
if ( Tree.FindNearestRayTriangleIntersection ( MouseRay, HitDistance, HitTriangleID, BaryCoords ) )
{
// 메시와 충돌!
FVector3d HitPosition = MouseRay.PointAt( HitDistance );
}메시 부울 연산에서의 활용
// MeshBoolean.cpp에서 사용
FDynamicMeshAABBTree3 Spatial[ 2 ];
Spatial[ 0 ].SetMesh( Meshes[ 0 ] );
Spatial[ 0 ].Build();
Spatial[ 1 ].SetMesh( Meshes[ 1 ] );
Spatial[ 1 ].Build();
// 두 메시의 교차 확인
bool bIntersects = Spatial[ 0 ].TestIntersection( &Spatial[ 1 ] );디버깅 및 검증
트리 유효성 검사
bool IsValid( bool bAllowUnsafeModifiedMeshQueries ) const
{
if ( RootIndex < 0 )
return false;
// 메시가 변경되었는지 확인
if ( !bAllowUnsafeModifiedMeshQueries )
return ( MeshChangeStamp == Mesh->GetChangeStamp() );
return true;
}주의사항
| 상황 | 설명 |
|---|---|
| 메시 수정 | 메시를 수정하면 트리가 무효화됨 |
| 무효화된 트리 쿼리 | 잘못된 결과 발생 |
| 해결 방법 | 메시 수정 후 Build() 재호출 필요 |
핵심 요약
| 특징 | 설명 |
|---|---|
| 자료구조 | 이진/단일 자식 트리 ( Binary/Unary Tree ) |
| 목적 | 빠른 공간 쿼리 ( O(log n) ) |
| 저장 방식 | 플랫 배열 ( 포인터 없음, 캐시 친화적 ) |
| 주요 쿼리 | 최근접 삼각형, 레이 교차, 메시 교차 |
| 구축 방법 | Top-Down 중간점 분할 |
| 최적화 | 가지치기, 가까운 자식 우선, Early Exit |
장점
| 특징 | 설명 |
|---|---|
| 빠른 쿼리 성능 | O(log n) 시간 복잡도 |
| 메모리 효율 | 포인터 없는 플랫 배열 구조 |
| 다양한 쿼리 | 최근접, 레이캐스팅, 교차 검사 등 |
| 정확한 결과 | 수치 안정성 보장 |
단점
| 특징 | 설명 |
|---|---|
| 구축 비용 | 메시 수정마다 재구축 필요 |
| 동적 업데이트 불가 | 정적 메시용 자료구조 |